
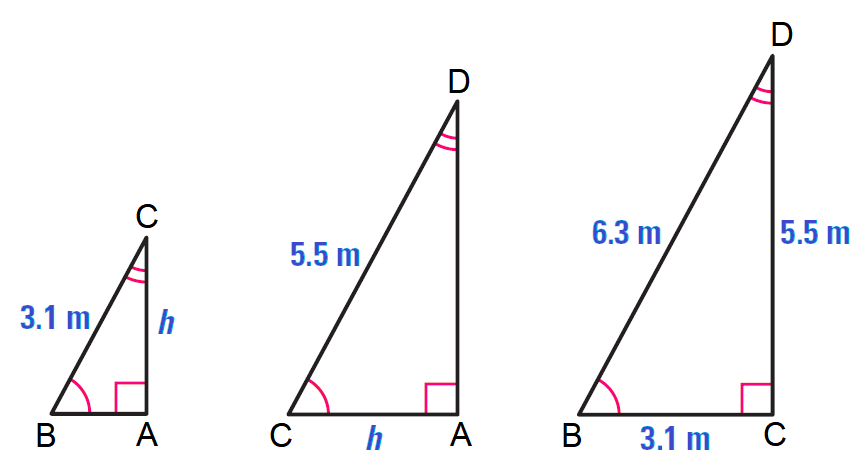

Some of them have different sizes and some of them have been turned or flipped.Īll corresponding sides have the same ratioĪlso notice that the corresponding sides face the corresponding angles. To find the geometric mean of two numbers, just find the product of those numbers and take the square root Follow along with this tutorial to learn the process. (Equal angles have been marked with the same number of arcs) If one of the acute angles of a right triangle is congruent to an acute angle of another right triangle, then by Angle-Angle Similarity the triangles are. What is the height of the cliff to the nearest foot? The cliff is about 142.5 + 5.5, or 148 ft high.Two triangles are Similar if the only difference is size (and possibly the need to turn or flip one around). Check it out!!! A surveyor positions himself so that his line of sight to the top of a cliff and his line of sight to the bottom form a right angle as shown.What is the height of the tree to the nearest meter? The tree is about 38 + 1.6 = 39.6, or 40 m tall Because the two are similar triangles, is the hypotenuse of the second triangle, and is its longer leg. is the hypotenuse of the first triangle since one of its legs is half the length of that hypotenuse, is 30-60-90 with the shorter leg and the longer. Her eyes are about 1.6 m above the ground, and she is standing 7.8 m from the tree. Correct answer: Explanation: Since and is a right angle, is also a right angle. Example 4: Measurement Application To estimate the height of a Douglas fir, Jan positions herself so that her lines of sight to the top and bottom of the tree form a 90 angle.Check It Out! Example 3 Find u, v, and w.Example Example 3: Finding Side Lengths in Right Triangles Find x, y, and z.A Pythagorean triple is a group of three whole Numbers that satisfies the equation a2+b2c2 where c is the greatest number. All the relationships in red involve geometric means. Solve for x and y y x2(8)(5) X6.3 y2(13)(8) y10.2 4. Similarity in right triangles You can use Theorem 8-1-1 to write proportions comparing the side lengths of the triangles formed by the altitude to the hypotenuse of a right triangle.If necessary, give the answer in simplest radical form. Check it out!! Find the geometric mean of each pair of numbers.Example Find the geometric mean of each pair of numbers.4 and 25 Solution Let x be the geometric mean. Example 2A: Finding Geometric Means Find the geometric mean of each pair of numbers.

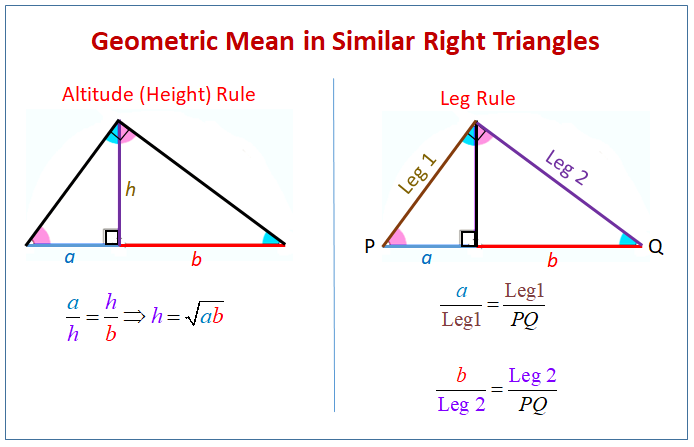
So the geometric mean of a and b is the positive number x such that, or x 2 = ab. The geometric mean of two positive numbers is the positive square root of their product. In this case, the means of the proportion are the same number, and that number is the geometric mean of the extremes.
Geometric Mean-Altitude Theorem 1The length of the altitude to. • Geometric mean Consider the proportion. Right Triangle Similarity Theorem
The altitude to the hypotenuse of a right.
Check it out Write a similarity statement comparing the three triangles By Theorem 8-1-1, LJK ~ JMK ~ LMJ.Solution Sketch the three right triangles with the angles of the triangles in corresponding positions.Example #1 Write a similarity statement comparing the three triangles.Similarity in right triangles In a right triangle, an altitude drawn from the vertex of the right angle to the hypotenuse forms two right triangles.Apply similarity relationships in right triangles to solve problems. If the altude is drawn to the hypotenuse of a right triangle, then the 2 s formed are similar to the original and to each other.


 0 kommentar(er)
0 kommentar(er)
